アクティブフィルタを導入した場合に系統が不安定になり、運転不能になることがあるという報告がありますが、どのような現象なのでしょうか、その対応策および注意事項について教えて下さい。
実際の配電線では線路のインピーダンスがあり、負荷側には進相コンデンサがつながれているので、アクティブフィルタ (Active Filter:AF) を実際に配電線に接続すると一種の不安定現象が起きて運転不能になることが報告されている。
1.AFの不安定現象
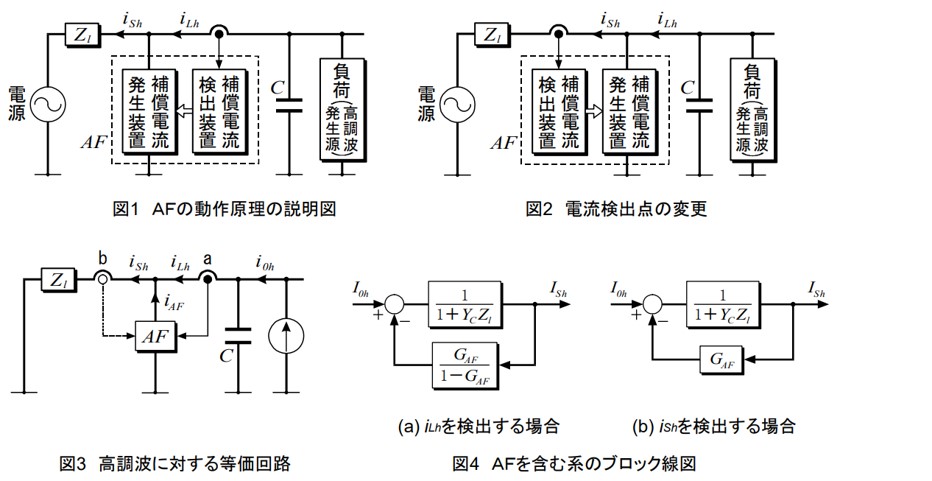
図1 は、配電用AFの原理の説明図である。負荷電流から、配電系統にとって障害となる電流iLhを検出し、これと逆位相の電流 (-iLh) を補償電流発生装置(変換器)で生成し、線路に供給する。
この動作が正確かつ時間遅れなく行われれば、図中で ish=iLh-iLh= 0 となり、AFの設置点から電源側の配電線への障害電流の流出は阻止できる。 これがAFの基本的な考え方であるが、実際の系統で線路インピーダンスが無視できないときは、次のような問題が生じる。
AFから線路をみたインピーダンスを Zl とし、また、AFの設置点の近傍に進相コンデンサが付設されていると仮定する。 もし、Zl = 0(線路が無限大母線)ならば、AFが供給する電流はすべて電源側の枝路を流れるので問題ない。しかし、Zl が無視できないときは、-iLh の一部が進相コンデンサ(高調波に対してインピーダンスが小さい) に分流する。 この結果、検出点の高調波電流は、AFが動作することにより逆に増加する場合が起こり得る。
AFはこの電流を補償すべく動作するので、これがコンデンサ電流をさらに増加させる。つまり、制御でいう “正帰還動作” が行われて、系が不安定になる場合がある。なお、補償電流の演算処理による時間遅れが生じる場合も不安定現象はより起こりやすくなる。
2.電流検出点の変更によるAFの安定化
上に述べたような不安定現象を回避するには、図2 のように線路電流 ish を検出し、ish= 0 となるようなフィードバック制御を行えばよい。AFが時間遅れなく正確に動作すれば、進相コンデンサが近くに付設されており、Zl が無視できない線路でも、AFは安定に動作し所期の目的が達成できる。
まず、AFを含む系の伝達関数を求める。図3 は、高調波電流に対する等価回路である。図から回路方程式は 式(1) のようになる。 ただし,YC は進相コンデンサのアドミタンス,GAF はAFのゲインを表す。この場合,理想的には GAF ≒ 1 である。
式(1) から、伝達関数 Ish(s)/Ioh(s) を求めると、式(2) のようにる。 これより、図4(a) のブロック線図が得られる。 式(2) または 図4(a) から、系が安定であるためには、GAF< 1 でなければならない。 (GAF > 1 のときは正帰還になり系は不安定になる。 また,AFに演算などによる時間遅れがあると,GAF < 1 であっても系が不安定になる可能性がある。)
次に、図3 で補償電流検出点を b 点に移したときの伝達関数を求める。 このときAFが供給する電流は-iLhではなく、ishをGAF倍したものである。 従って、式(1) と異なるのは、iAF=-GAF ・ish だけであり、これから伝達関数は 式(3) のようになる。 また、ブロック線図は 図4(b) のようになる。
次に求めた伝達関数において、AFの制御時間遅れがどう影響するか考えてみる。AFの制御時間遅れを表すため、GAF=Ke-Ts とする。 また、簡単のため、YC とZl を 式(4) 次のように仮定する。
ここで、Zl(s) はAFから配電線をみたインピーダンスで、線路のLとRではないことに注意する。すなわち、配電線には多くの負荷が接続されているので、それらを合成した(等価な)LとRを考える必要がある。遅れ時間Tが微小であれば,ゲインKを大きくしても系は不安定にはならない。

(名古屋工業大学 准教授 青木 睦 記)